Following Dr NICOLA SCAFETTA

Dr Nicola Scafetta

was my first connection and inspiration for cycle research and analysis

A master at his work!! Prolific researcher and defender of solar system dynamics and the earths climate
I should have stared this post ages ago!!

His home page
https://www.docenti.unina.it/ricerca/visualizzaPubblicazioni.do?idDocente=4e49434f4c4153434146455454415343464e434c36395432364437303855&nomeDocente=NICOLA&cognomeDocente=SCAFETTA

CLICK ON THE TITLE TOLOAD ALL FURTHER ENTRIES AT THE BASE OF THIS PAGE

Dr Scafetta reconciles the earths climate to solar system dynamics and maybe a tad of AGW
I hope to summarize all of these in the future in the comments section below
but for now some links

Here is a taste of some of his recent work
—————————————————————

2014..
The complex planetary synchronization structure of the solar system

N. Scafetta
http://www.pattern-recogn-phys.net/2/1/2014/prp-2-1-2014.html
Downloaded from the pdf

Click to access prp-2-1-2014.pdf

EXTRACTS…(I have extracted information for my interest and is not in order/sequence)

The complex planetary synchronization structure of the solar system

N. Scafetta 2014
http://www.pattern-recogn-phys.net/2/1/2014/prp-2-1-2014.html
—————————————————————-
From 1596 to 1619 Kepler formulated preliminary mathematical relations of approximate commensurabilities among the planets, which were later re- formulated in the Titius–Bode rule (1766–1772), which successfully predicted the orbital position of Ceres and Uranus.
..
(1) the planetary orbital periods can be approximately deduced from a simple system of resonant frequencies;

(2) the solar system oscillates with a specific set of gravitational frequencies, and many of them (e.g., within the range between 3yr and 100yr) can be approximately con- structed as harmonics of a base period of ∼178.38yr; and
(3) solar and climate records are also characterized by planetary harmonics from the monthly to the millennial timescales.
The general conclusion is that the solar system works as a resonator characterized by a specific harmonic planetary structure that also synchronizes the Sun’s activity and the Earth’s climate.
—————–
https://picasaweb.google.com/110600540172511797362/SOLARSYSTEMAndClimate#6042906737291319810

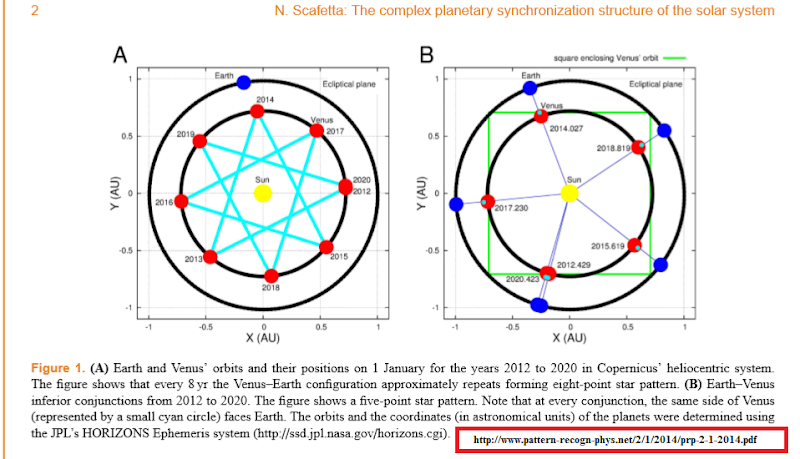
In fact, as Fig. 1b shows, in one synodic period Earth revolves 1.59867 times around the Sun, while Venus rotates on its own axis 2.40277 times in the opposite direction.
The sum of the fractional part of the two numbers is almost exactly 1 (∼1.00144). Thus, not only is Earth almost synchronized with Venus in a 8 : 13 or- bital resonance and in a 8 : 5 synodic resonance

the 27.3 days sidereal orbital period of the Moon around Earth appears well synchronized with the 27.3 days period of the Carrington rotation of the Sun,as seen from the Earth, which determines a main electromagnetic oscillation of the heliospheric current sheet in a Parker spiral.

The collective synchronization among all celestial bodies in our solar system indicates that they interact energetically with each other and have reached a quasi-synchronized dynamical state.

As discovered by Christian Huygens in the 17th century, entrainment or synchronization between coupled oscillators requires very little energy exchange if enough time is allowed.

Huygens patented the first pendulum clock and first noted that, if hung on the same wall, after a while, pendulum clocks synchronize to each other due to the weak physical coupling induced by small harmonic vibrations propagating in the wall (Pikovsky, 2001).

.. the Earth’s gravity or some other planetary mechanism has synchronized the rotation of Venus with Earth, the planets could have synchronized the internal dynamics of the Sun, and therefore they could be modulating solar activity.

Thus, the Earth’s climate could be modulated by a complex harmonic forcing consisting of
(1) lunar tidal oscilla- tions acting mostly in the ocean;
(2) planetary-induced so- lar luminosity and electromagnetic oscillations modulating mostly the cloud cover, and therefore the Earth’s albedo; and
(3) a gravitational synchronization with the Moon and other planets of the solar system modulating, for example, the Earth’s orbital trajectory and its length of day (cf. Mörner, 2013).

The planetary rhythm of the Titius–Bode rule
Titius (1766) and later Bode (1772) noted that the semi-major axes an of the planets of the solar system are function of the planetary sequence number n. Adding 4 to the series 0, 3, 6, 12, 24, 48, 96, 192 and 384 and
dividing the result by 10 gives a series that approximately reproduces the semi-major axis length of the planets in astronomical units (1AU = Sun– Earth average distance).

4 The asteroid belt “mirror” symmetry rule
———————————————–
A curious mathematical relationship linking the four terrestrial inner planets (Mercury, Venus, Earth and Mars) and the four giant gaseous outer planets (Jupiter, Saturn, Uranus and Neptune) exists (Geddes and King-Hele, 1983). The semi-major axes of these eight planets appear to reflect about the asteroid belt. This mirror symmetry associates Mercury with Neptune, Venus with Uranus, Earth with Saturn and Mars with Jupiter.

Me×Ea Ve×Ma ≈ Ju×Ur Sa×Ne

These relations relate the four inner and the four outer planets of the solar system.
Even if the Geddes and King-Hele rule is not perfect, it does suggest the existence of a specific ordered structure in the planetary system where the asteroid belt region acts as a kind of mirroring boundary condition between the inner and outer regions of the solar system.

5 The matrix of planetary resonances
—————————————-
Molchanov (1968, 1969a) showed that the periods of the planets could be approximately predicted with a set of sim- ple linear equations based on integer coefficients describing the mutual planetary resonances.
The gravitational harmonics of the solar system
———————————————————–
Several spectral peaks can be recognized, such as
-the ∼1.092yr period of the Earth–Jupiter conjunctions;
-the ∼9.93 and ∼19.86yr periods of the Jupiter–Saturn spring (half synodic) and synodic cycles,
respectively;
-the ∼11.86, ∼29.5, ∼84 and ∼165yr orbital period of Jupiter, Saturn, Uranus and Neptune,
respectively;
– the ∼61yr cycle of the tidal beat between Jupiter and Saturn;
and
– the periods corresponding to the synodic cycle between Jupiter and Neptune (∼12.8yr), Jupiter and Uranus (∼13.8yr), Saturn and Nep- tune (∼35.8yr), Saturn and Uranus (∼45.3), and Uranus and Neptune (∼171.4yr),
as well as many other cycles including the spring (half-synodic) periods.

Additional spectra peaks at ∼200–220, ∼571, ∼928 and ∼4200yr are also observed.

Clustered frequencies are typically observed. For example, the ranges 42–48yr, 54–70yr, 82–100yr (Gleissberg cycle) and 150–230yr (Suess–de Vries cycle) are clearly observed in Fig. 4 and are also found among typical main solar activity and aurora cycle frequencies (Ogurtsov et al., 2002; Scafetta and Willson, 2013a).

https://picasaweb.google.com/110600540172511797362/SOLARSYSTEMAndClimate#6042929093474072546

7 The planetary synchronization and modulation of the ∼11yr solar cycle
———————————————————————————————
Hung (2007) also reported that 25 of the 38 largest known solar flares were observed to start when one or more tide- producing planets (Mercury, Venus, Earth, and Jupiter) were either nearly above the event positions (less than 10 deg. lon- gitude) or at the opposing side of the Sun.

The first model relating the 11yr solar cycle to the con- figuration of Venus, Earth and Jupiter was proposed by Bendandi (1931); later Bollinger (1952), Hung (2007) and others developed equivalent models.

It was observed that Venus, Earth and Jupiter are the three major tidal planets (e.g., Scafetta, 2012c).

By taking into account the combined alignment of Venus, Earth and Jupiter, it is easy to demonstrate that the gravitational configuration of the three planets repeats every 22.14 yr

Moreover, because the configurations Ea–Ve–Sun–Ju and Sun–Ve–Ea–Ju are equivalent about the tidal potential, the tidal cycle presents a recurrence of half of the above value (i.e., a period of 11.07yr). This is the average solar cycle length observed since 1750 (e.g., Scafetta, 2012b).

Figure 5 shows that a measure based on the most aligned days among Venus, Earth and Jupiter is well correlated, in phase and frequency, with the ∼11yr sunspot cycle: for details about the Venus–Earth–Jupiter 11.07yr cycle see Battistini (2011, Bendandi’s model), Bollinger (1952), Hung (2007), Scafetta (2012c), Salvador (2013), Wilson (2013a) and Tattersall (2013).

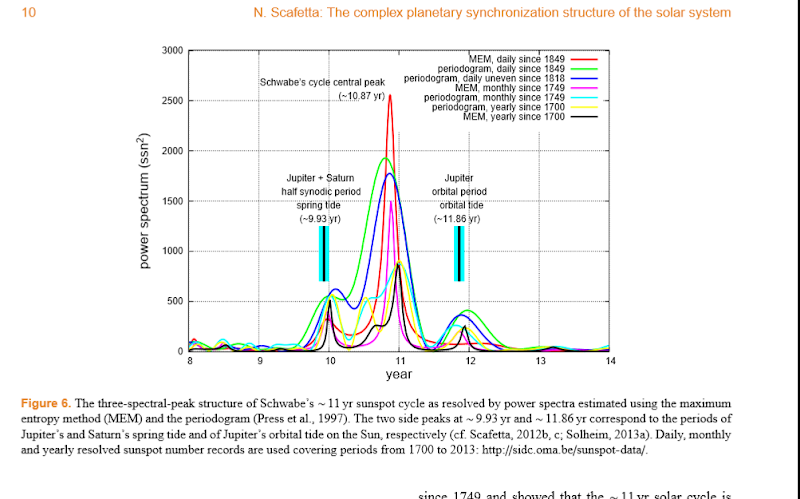
The main tides generated by Jupiter and Saturn on the Sun are characterized by two beating oscillations: the tidal oscillation associated with the orbital period of Jupiter (∼11.86yr period) and the spring tidal oscilla tion of Jupiter and Saturn (∼9.93yr period)

(Brown, 1900; Scafetta, 2012c). Scafetta (2012b, c) used de tailed spectral analysis of the sunspot monthly record since 1749 and showed that the ∼11yr solar cycle is constrained by the presence of two spectral peaks close to the two theoretical tidal periods deduced from the orbits of Jupiter and Saturn (see Fig. 6). These two frequencies modulate the main central cycle at ∼10.87yr period.

The beat generated by the superposition of the three harmonics is characterized by four frequencies at about 61, 115, 130, and 983yr periods that are typically observed in solar records (e.g., Ogurtsov et al., 2002; Scafetta, 2012b). Scafetta (2012b) proposed a harmonic model for solar variability based on three frequencies at periods of ∼9.93, ∼10.87 and ∼11.86yr.

Scafetta’s (2012b) three- frequency solar model forecasts that the Sun will experience another moderate grand minimum during the following decades and will return to a grand maximum Hemisphere covering the last 2000yr; and (4) the ∼59– 63yr oscillation observed in the temperature record since 1850 and other features. Scafetta’s (2012b) three- frequency solar model forecasts that the Sun will ex- perience another moderate grand minimum during the following decades and will return to a grand maximum
in the 2060s similar to the grand maximum experienced in the 2000s (see Fig. 7b).

When these harmonics interfere destructively the Sun enters into a prolonged grand minimum; when they in terfere constructively the Sun experiences a grand maximum.

The proposed semi-empirical and empirical harmonic so- lar models agree about the fact that the Sun is entering into a period of grand minimum. Indeed, the latest sunspot cy- cles #19–24 are closely correlated to the sunspot cycles #1– 5 immediately preceding the Dalton Minimum (1790–1830)

——————————————————————————————-

——————————————————————————————–

2014
Nicola Scafetta: Global temperatures and sunspot numbers. Are they related? Yes, but non linearly

http://www.sciencedirect.com/science/article/pii/S0378437114005226

” (B) Detail the semi-empirical astronomical model proposed by Scafetta [37]. The red curve shows the original global surface temperature record published in Scafetta [37]. The blue curve shows the same global surface temperature updated to the most current available month. The back curve within the cyan area is the semi-empirical astronomical model forecast (since 2000) that clearly outperforms the IPCC 2007 CMIP3 general circulation model projections (green area). The yellow curve is the harmonic component alone without the anthropogenic component. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)”

\Discussed here

Nicola Scafetta: Global temperatures and sunspot numbers. Are they related? Yes, but non linearly

———————————————————————————————–